Fundamentos
...no hay enseñanza más que
matemática, el resto es broma.
J. Lacan. ...ou pire

A lo largo de su enseñanza, Lacan ha empleado diversos conceptos provenientes de la Lógica, la Topología, la Teoría de Conjuntos y otras ramas de la Matemática. Sin pretender hacer una valoración de dicho empleo, podemos decir que no se trata de alusiones casuales, sino que el propio Lacan las consideró un elemento basal para la formación del analista, expresando de modo explícito que la formación no puede excluir a lo formal.

En el presente curso se desarrollan los principales aspectos matemáticos abarcados por Lacan a lo largo de sus seminarios, a excepción de la topología, que por su especial importancia y amplitud de temas ha merecido un curso específicamente dedicado a ella.

Las dos primeras clases están dedicadas a la Teoría de Conjuntos, cuya problemática constituye uno de los ejes fundamental en el recorrido lacaniano. Temas tales como la paradoja de Russell, el Universo, el lenguaje y los metalenguajes se ven reflejados en conceptos de suma importancia tales como el no todo, el objeto a, etcétera. Por otra parte, la construcción del número natural apoyada en el conjunto vacío es el objeto de aquella celebrada exposición de Recanati del Seminario 19. Veremos algunas nociones básicas de la teoría original de Cantor -denominada ingenua- y luego presentaremos, paso por paso, los axiomas de la teoría axiomática de conjuntos par excellence, desarrollada por Zermelo y Fraenkel a principios del siglo XX. En particular, esto nos permitirá comprender algunas cuestiones importantes como la del infinito actual y aquella célebre demostración diagonal, a la que Lacan se refiere en El saber del psicoanalista del siguiente modo: “me parece absolutamente maravillosa.”
Sin duda, esta y muchas otras “maravillas” son las que lo han llevado un día a anunciar: “Finalmente reduje el Psicoanálisis a la Teoría de Conjuntos.”

En la siguiente clase nos introduciremos en otros aspectos profundos de la Lógica y de los sistemas formales, como la de interpretación, verdad, consistencia, completitud, etcétera. Esto nos permitirá, en particular, hablar de las paradojas y los teoremas de Gödel, que en el pasado siglo revelaron su incidencia en el campo del lenguaje y el psicoanálisis. En cierto modo, la disyuntiva gödeliana entre incompletitud e inconsistencia puede ser contemplada, desde la perspectiva de la lógica clásica, como aquello que Lacan denominó una elección forzada.

Finalmente, las dos últimas clases están dedicadas a dos temas muy específicos, cuyos títulos resultarán muy familiares al estudioso del Seminario 14, La lógica del fantasma. Por un lado, veremos las nociones básicas de la estructura de grupo -entre cuyos ejemplos más sencillos se encuentra el grupo de Klein- y algunas aplicaciones al campo del lenguaje, abordado desde la borgeana biblioteca de Babel. Por otro lado, en la última clase presentaremos algunas propiedades de aquella cantidad que ha sido objeto de los más variados empleos, tanto en el arte como en la mística o la religión: el número de oro.

Este curso se basa en el libro del mismo título, publicado en 2001 por el sello Lectour y agotado hace ya muchos años.

Contenidos

Clase 1. Introducción a la teoría de conjuntos.

• Primera parte: Teoría Ingenua de Conjuntos y paradoja de Russell.
• Segunda parte: Introducción ingenua a la teoría no ingenua.
  1. Axioma de extensionalidad.
  2. Axioma del conjunto vacío.
  3. Axioma de separación.
  4. Axioma del par.
  5. Axioma del conjunto potencia.
  6. Axioma de unión.
  7. Axioma del infinito.
  8. Axioma de sustitución.
  9. Axioma de elección.
  10. Axioma de regularidad.

Clase 2. La obra del hombre.

• Introducción.
• Números Enteros y Racionales.
• Números Reales.
• Un "lapsus" de Euclides.
• La demostración diagonal de Cantor.

Clase 3. Interpretación, verdad, consistencia.

• Introducción.
• Un tiempo no estándar.
  • Sobre los modelos de la Lógica Temporal.
• Quine y las paradojas de la identificación.
  • El horror philosophiae.
  • Epiménides miente.
  • El Quijote de Lepanto.

Clase 4. La estructura de grupo.

• Introducción.
• Grupos, nada más.
• El grupo de Klein.
• Apéndice: Borges y la biblioteca de Babel.

Clase 5. El número de oro.

1. La "divina proporción".
2. 
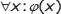3. Leonardo.
4. El nombre del Padre (una filiación provechosa).
5. 
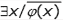6. Epílogo.